평형 상수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

평형 상수는 가역적인 화학 반응이 평형 상태에 도달했을 때, 반응물과 생성물의 농도 관계를 나타내는 상수이다. 이 값은 온도에 따라 변하며, 반응물 및 생성물의 초기 농도와는 무관하다. 평형 상수는 생성물의 몰농도 곱과 반응물의 몰농도 곱의 비로 정의되며, 값이 클수록 생성물이 반응물보다 더 많이 존재함을 의미한다. 평형 상수는 농도 평형 상수(Kc), 압력 평형 상수(Kp), 산 해리 상수(Ka), 염기 해리 상수(Kb), 용해도곱 상수(Ksp) 등 다양한 종류가 있으며, 반응 지수(Q)와 비교하여 반응의 진행 방향을 예측할 수 있다. 또한, 불균일 평형, 아레니우스 식, 동위원소 치환 효과 등 다양한 요소를 고려하여 평형 상수를 측정하고 계산할 수 있으며, 생화학 및 산업 분야에서 반응 조건 설정 및 수율 예측에 활용된다.

더 읽어볼만한 페이지

평형화학 - 헤모글로빈
헤모글로빈은 척추동물 혈액에서 산소를 운반하는 주요 단백질로, 헴과 글로빈이 결합된 4개의 소단위체로 구성된 사량체 구조를 가지며, 헴의 철 성분이 산소와 결합하여 폐에서 조직으로 산소를, 조직에서 이산화탄소와 양성자를 운반하고, 산소 결합은 여러 요인에 의해 영향을 받으며, 유전자 돌연변이는 헤모글로빈병증을 유발하고, 농도와 기능은 질병 진단에 활용되며, 다양한 생물종에서 발견된다.
평형화학 - 해리 (화학)
해리는 분자, 복합체, 또는 이온이 더 작은 구성 요소로 분리되는 과정을 의미하며, 해리 상수는 화학 평형 상태에서 반응의 정도를 측정하는 데 사용된다.

평형 상수

2. 정의

굴트베르크^no(C. M. Gouldberg)와 보게^no(P. Waage)가 1864년에 질량 작용의 법칙을 제안하면서 평형 상수의 개념이 확립되었다.^[1]

일반적인 가역 반응에서 평형 상수는 다음과 같이 정의된다.

: $\alpha\,\mathrm{A} + \beta\,\mathrm{B} + \cdots \rightleftharpoons \rho\,\mathrm{R} + \sigma\,\mathrm{S} + \cdots$

: $K^\ominus = \frac{\mathrm{\{R\}}^\rho \mathrm{\{S\}}^\sigma...}{\mathrm{\{A\}}^\alpha \mathrm{\{B\}}^\beta...}= \frac{[\mathrm{R}]^\rho [\mathrm{S}]^\sigma ...}{[\mathrm{A}]^\alpha [\mathrm{B}]^\beta ...} \times \Gamma,$

: $\Gamma= \frac{\gamma_R^\rho \gamma_S^\sigma...}{\gamma_A^\alpha \gamma_B^\beta...},$

여기서 {X}는 평형 상태에서 시약 X의 열역학 활동도를, [X]는 해당 농도(몰/리터)의 수치 값을,^[3] γ는 해당 활동도 계수를 나타낸다. X가 기체인 경우, [X] 대신 압력 단위인 bar로 표시된 분압 $P_X$ 의 수치 값을 사용한다.^[3]

평형 상수는 표준 깁스 자유 에너지 반응 변화 $\Delta G^\ominus$ 와 다음과 같은 관계를 갖는다.

: $\Delta G^\ominus = -RT \ln K^\ominus,$

여기서 ''R''은 기체 상수, ''T''는 절대 온도(단위: 켈빈)이다.

평형 상수는 평형에 도달하는 데 관여하는 반응의 정반응 및 역반응 속도 상수인 ''k''_f 및 ''k''_r과 다음과 같은 관계를 갖는다.

: $K^\ominus = \frac{k_\text{f}}{k_\text{r}}.$

화학양론 계수 $\nu_i$ 로 표현되는 화학 반응에서 표준 평형 상수는

: $K^\circ =\exp\left[ -\sum_i \frac{\nu_i\, \mu_i^\circ(T)}{RT} \right]$

로 정의된다. 여기서 $\mu_i^\circ$ 는 표준 화학 퍼텐셜이다. 표준 절대 활동도 $\lambda_i^\circ =e^{\mu_i^\circ/RT}$ 를 사용하면

: $K^\circ =\prod \left[ \lambda_i^\circ(T) \right]^{-\nu_i}$

가 된다.

예를 들어

: $\nu_\text{A} \text{A} + \nu_\text{B} \text{B} \rightleftharpoons \nu_\text{C} \text{C} + \nu_\text{D} \text{D}$

로 표현되는 화학 반응에서는

: $K^\circ = \frac{ (\lambda_\text{A}^\circ)^{\nu_\text{A}} (\lambda_\text{B}^\circ)^{\nu_\text{B}}}{ (\lambda_\text{C}^\circ)^{\nu_\text{C}} (\lambda_\text{D}^\circ)^{\nu_\text{D}} }$

이 된다.

화학양론 계수 $\nu_i$ 로 표현되는 이상 기체의 화학 반응에서, 압력 $p$ 및 몰분율 $x_i$ 에서의 압력 평형 상수는

: $K_p =\prod \left[ \frac{x_i p}{p^\circ} \right]^{\nu_i}$

로 정의된다. 여기서 $p^\circ$ 는 표준 상태 압력이다. 표준 상태 압력은 일반적으로 $1=p^\circ = 1 \text{bar}$ 또는 $1=p^\circ = 1 \text{atm}$ 로 선택된다.

앞서 언급된 화학 반응의 경우 압력 평형 상수는

: $K_p = \left( \frac{x_\text{C} p}{p^\circ} \right)^{\nu_\text{C}} \left( \frac{x_\text{D} p}{p^\circ} \right)^{\nu_\text{D}}\bigg/ \left( \frac{x_\text{A} p}{p^\circ} \right)^{\nu_\text{A}} \left( \frac{x_\text{B} p}{p^\circ}\right)^{\nu_\text{B}}$

가 된다.

실제 기체의 경우 분압을 퓨가시티로 대체하여

: $K_p =\prod \left[ \frac{f_i(x;T,p)}{p^\circ} \right]^{\nu_i}$

가 된다.

화학량론 계수 $\nu_i$ 로 표현되는 이상용액의 용질의 화학 반응에서, 몰농도 $c_i$ 에서의 농도 평형 상수는

: $K_c =\prod \left[ \frac{c_i}{c^\circ} \right]^{\nu_i}$

로 정의된다. 여기서 $c^\circ$ 는 표준 몰농도이다. 표준 몰농도는 일반적으로 $1=c^\circ=1 \text{mol/L}$ 로 선택된다.

위 화학 반응의 경우 압력 평형 상수는

: $K_c = \left( \frac{c_\text{C}}{c^\circ} \right)^{\nu_\text{C}} \left( \frac{c_\text{D}}{c^\circ} \right)^{\nu_\text{D}}\bigg/ \left( \frac{c_\text{A}}{c^\circ} \right)^{\nu_\text{A}} \left( \frac{c_\text{B}}{c^\circ}\right)^{\nu_\text{B}}$

가 된다.

실제 용액의 경우 농도를 상대 활량으로 대체하여

: $K_c =\prod \left[ a_{c,i}(c;T,p) \right]^{\nu_i}$

가 된다.

2. 1. 기본 정의

가역적인 화학 반응이 특정 온도에서 평형을 이루고 있을 때, 반응물과 생성물의 농도 관계를 나타내는 상수를 말한다. 반응물 및 생성물의 초기 농도에 관계없이 평형 상수는 항상 같은 값을 가진다. 이 값이 크면 평형 상태에서 생성물이 반응물보다 더 많이 존재함을 의미한다.^[1] 평형 상수는 화학 평형의 법칙으로부터 유도된 것으로, 생성물의 몰농도 곱과 반응물의 몰농도 곱의 비로 나타낸다. 평형 상수가 크면 정반응이 활발하여 생성 물질이 많이 존재하고, 화학 반응식의 계수가 변하면 평형 상수 값도 변한다. 평형 상수는 온도에만 영향을 받고, 압력이나 농도에는 영향을 받지 않는다.

반응물 A와 B가 반응하여 생성물 C와 D를 생성하는 가역 반응에 대한 화학 반응식은 다음과 같다.

:

aA + bB \leftrightarrows cC + dD

(여기서

a, b, c, d

는 반응 계수)

이러한 가역 반응은 일정한 온도에서 충분한 시간이 지나면 반응물이나 생성물의 초기 농도에 관계없이 겉보기 농도에 변화가 없는 평형 상태에 이르게 된다. 이러한 평형 상태에서 반응물과 생성물의 농도 비는 일정하며, 이 값을

K_c

(평형 상수)라고 한다. 아래 첨자 c는 농도(concentration)를 나타낸다.

:

K_c=\frac{[C]^c [D]^d}{[A]^a [B]^b}

여기서

[A], [B], [C], [D]

는 평형 상태에서 A, B, C, D의 몰 농도를 의미한다.

1864년 노르웨이의 굴드베르그와 보게는 이러한 관계를 질량 작용의 법칙(law of mass action)으로 제안하였다.^[1] 평형 상수는 실험적으로 결정하며, 화학 평형식에 따라 단위가 달라질 수 있지만, 관례적으로 평형 상수의 단위는 생략한다. 평형 상수 값은 온도에 따라 변하며, 화학 반응식의 계수에 의존한다.

열역학적 평형 상수(

K^\ominus

)는 정반응과 역반응의 속도가 같을 때의 반응 지수(

Q_t

) 값으로 정의된다.^[1]^[2] 화학 평형 상태에서는 혼합물의 화학적 조성이 시간에 따라 변하지 않으며, 반응에 대한 깁스 자유 에너지 변화(

\Delta G

)는 0이다. 평형 상수(

K^\ominus

)는 평형 상태의 혼합물 조성과 다음과 같은 관계를 갖는다.

:

K^\ominus = \frac{\mathrm{\{R\}}^\rho \mathrm{\{S\}}^\sigma...}{\mathrm{\{A\}}^\alpha \mathrm{\{B\}}^\beta...}= \frac.

2. 2. 열역학적 정의

표준 평형 상수(

K^\ominus

)는 표준 상태 깁스 자유 에너지 변화(

\Delta G^\ominus

)와 다음과 같은 관계를 갖는다.^[1]^[2]

:

\Delta G^\ominus = -RT \ln K^\ominus,

여기서 ''R''은 기체 상수, ''T''는 절대 온도(단위: 켈빈)이며,

\ln

은 자연 로그이다.

일반적인 화학 반응식은 다음과 같이 나타낼 수 있다.

:

\alpha\,\mathrm{A} + \beta\,\mathrm{B} + \cdots \rightleftharpoons \rho\,\mathrm{R} + \sigma\,\mathrm{S} + \cdots

이때 열역학적 평형 상수

K^\ominus

는 다음과 같이 정의된다.

:

K^\ominus = \frac}^\rho \mathrm{\{S\}}^\sigma...}}}^\alpha \mathrm{\{B\}}^\beta...}}

여기서 {X}는 평형 상태에서 시약 X의 열역학 활동도를 나타낸다. 즉, 활동도를 사용하여 평형 상수를 나타낼 수 있다.^[1]^[2]

또한, 용액 내 화학에서는 결합 상수와 같은 의미로 사용되기도 한다.^[22]

3. 평형 상수의 종류

다양한 화학 평형 상태를 나타내기 위해 여러 종류의 평형 상수가 사용된다.

누적 상수 (''β''): 시약으로부터 착물이 형성되는 반응에 대한 상수이다. 예를 들어, ML₂ 형성에 대한 누적 상수는 다음과 같이 표현된다.

::M + 2 L ML₂; [ML₂] = ''β''₁₂[M][L]²

단계적 상수 (''K''): ML과 L로부터 같은 착물이 형성되는 반응에 대한 상수이다.

::ML + L ML₂; [ML₂] = ''K''[ML][L] = ''Kβ''₁₁[M][L]²

따라서, ''β''₁₂ = ''Kβ''₁₁ 관계가 성립하며, 누적 상수는 항상 단계적 상수의 곱으로 표현될 수 있다.

유기화학 및 생화학에서는 산 해리 평형에 대해 p''K''_a 값을 사용하는 것이 일반적이다.

:

\mathrm{p}K_\mathrm{a}=-\log K_{\mathrm{diss}} = \log \left(\frac{1}{K_\mathrm{diss}}\right)\,

여기서 ''log''는 상용로그를 나타내고, ''K''_diss는 단계적인 산 해리 상수이다. 염기의 경우 염기 결합 상수인 p''K''_b를 사용하며, p''K''_a + p''K''_b = p''K''_w 관계가 있으므로, 계산에는 항상 p''K''_a를 사용할 수 있다.

반면, 금속 착물의 안정도 상수와 포접 착물의 결합 상수는 일반적으로 결합 상수로 표현된다.

예를 들어 니트릴로트리아세트산(NTA, N(CH₂CO₂H)₃)을 H₃L로 지정하고, 금속 이온 M과 ML 및 MHL 착물을 형성하는 경우, 해리 상수는 다음과 같이 표현된다.

:

\begin{array}{ll}\ce{H3L <=> {H2L} + H}; & \ce{p}K_1=-\log \left(\frac{[\ce{H2L}][\ce{H}]} {[\ce{H3L}]} \right)\\\ce{H2L <=> {HL} + H}; & \ce{p}K_2=-\log \left(\frac{[\ce{HL}][\ce{H}]} {[\ce{H2L}]} \right)\\\ce{HL <=> {L} + H}; & \ce{p}K_3=-\log \left(\frac{[\ce{L}][\ce{H}]} {[\ce{HL}]} \right)\end{array}

누적 결합 상수는 다음과 같이 표현할 수 있다.

:

\begin{array}{ll}\ce{{L} + H <=> HL}; & \log \beta_{011} =\log \left(\frac{[\ce{HL}]}{[\ce{L}][\ce{H}]} \right)=\ce{p}K_3 \\\ce{{L} + 2H <=> H2L}; & \log \beta_{012} =\log \left(\frac{[\ce{H2L}]}{[\ce{L}][\ce{H}]^2} \right)=\ce{p}K_3+\ce{p}K_2 \\\ce{{L} + 3H <=> H3L}; & \log \beta_{013} =\log \left(\frac{[\ce{H3L}]}{[\ce{L}][\ce{H}]^3} \right)=\ce{p}K_3+\ce{p}K_2+\ce{p}K_1 \\\ce{{M} + L <=> ML}; & \log \beta_{110} =\log \left(\frac{[\ce{ML}]}{[\ce{M}][\ce{L}]} \right)\\\ce{{M} + {L} + H <=> MLH}; & \log \beta_{111} =\log \left(\frac{[\ce{MLH}]}{[\ce{M}][\ce{L}][\ce{H}]} \right)\end{array}

3. 1. 농도 평형 상수 (Kc)

가역적인 화학 반응에서 특정 온도에서 평형을 이룰 때, 반응물과 생성물의 농도 관계를 나타내는 상수이다. 이 값은 반응물 및 생성물의 초기 농도에 관계없이 항상 일정하며, 크면 평형에서 생성물이 반응물보다 더 많이 존재함을 의미한다. 평형 상수는 화학 평형의 법칙으로부터 유도된 것으로, 생성물의 몰농도 곱과 반응물의 몰농도 곱의 비이다.^[1]

일반적인 화학 반응식은 다음과 같이 표현할 수 있다.

:

\alpha\,\mathrm{A} + \beta\,\mathrm{B} + \cdots \rightleftharpoons \rho\,\mathrm{R} + \sigma\,\mathrm{S} + \cdots

이때, 농도 평형 상수(

K_c

)는 다음과 같이 정의된다.

:

K_c = \frac{[\mathrm{R}]^\rho [\mathrm{S}]^\sigma ...}{[\mathrm{A}]^\alpha [\mathrm{B}]^\beta ...}.

여기서 [X]는 평형 상태에서 시약 X의 몰 농도를 나타낸다.

K_c

는 온도의 영향을 받지만, 압력이나 농도에는 영향을 받지 않는다.^[1]

K_c

는 열역학적 평형 상수(

K^\ominus

)와 활동도 계수(

\Gamma

)를 이용하여 다음과 같이 나타낼 수도 있다.

:

K_c = K^\ominus/\Gamma = \frac{[\mathrm{R}]^\rho [\mathrm{S}]^\sigma ...}{[\mathrm{A}]^\alpha [\mathrm{B}]^\beta ...}.

이는 표준 깁스 자유 에너지 변화(

\Delta G^\ominus

)와 다음과 같은 관계를 갖는다.

:

\Delta G^\ominus = -RT \ln K^\ominus,

여기서 R은 기체 상수, T는 켈빈 단위의 절대 온도이다.

이상용액의 용질의 화학 반응에서, 몰농도 에서의 농도 평형 상수는

:

K_c =\prod \left[ \frac{c_i}{c^\circ} \right]^{\nu_i}

로 정의된다. 여기서

c^\circ

는 표준 몰농도이며, 일반적으로

c^\circ = 1\mathrm{mol/L}

로 선택된다.

위 화학 반응의 경우 압력 평형 상수는

:

K_c = \left( \frac{c_\text{C}}{c^\circ} \right)^{\nu_\text{C}} \left( \frac{c_\text{D}}{c^\circ} \right)^{\nu_\text{D}}\bigg/ \left( \frac{c_\text{A}}{c^\circ} \right)^{\nu_\text{A}} \left( \frac{c_\text{B}}{c^\circ}\right)^{\nu_\text{B}}

가 된다.

실제 용액의 경우 농도를 상대 활량으로 대체하여

:

K_c =\prod \left[ a_{c,i}(c;T,p) \right]^{\nu_i}

가 된다.

또한, 용액 내 화학에서는 결합 상수와 같은 의미로 사용되고 있다.^[22]

3. 2. 압력 평형 상수 (Kp)

기체 상태의 물질이 평형을 이루고 있을 때, 농도 대신 각 성분 기체의 부분압력을 사용하여 나타낸 평형 상수를 압력 평형 상수(K_p)라고 한다. 이상기체에 가까운 경우, 압력 평형 상수는 농도 평형 상수와 비례하므로 화학 현상을 설명하는 데 문제가 없다.^[1]

가역적 화학 반응 aA + bB \leftrightarrows cC + dD이 평형에 도달했을 때, 압력 평형 상수 K_p는 다음과 같이 나타낼 수 있다.

:

K_P = \frac{[P_C]^c [P_D]^d}{[P_A]^a [P_B]^b}

K_p: 압력 평형 상수
p_A, p_B, p_C, p_D: 각 물질의 부분압

농도로 나타낸 평형 상수는 K_c로 표시하며, 이상 기체의 경우 다음과 같은 관계가 성립한다.

:

C=\frac{n}{V}=\frac{P}{RT}

따라서 농도 평형 상수와 압력 평형 상수 사이에는 다음과 같은 관계가 성립한다.

:K_p = K_c(RT)^Δn

Δn = (c+d)-(a+b): 생성물의 계수 합에서 반응물의 계수 합을 뺀 값

기체 평형의 경우, 농도 평형 상수는 압력 평형 상수에 비례한다. 기체의 경우 농도보다 부분압을 사용하는 것이 더 편리하므로 압력 평형 상수를 주로 사용한다.^[1]

이상 기체의 화학 반응에서, 압력 및 몰분율에서의 압력 평형 상수는 다음과 같이 정의된다.

:

K_p =\prod \left[ \frac{x_i p}{p^\circ} \right]^{\nu_i}

여기서

p^\circ

는 표준 상태 압력으로, 일반적으로

1=p^\circ = 1 bar

또는

1=p^\circ = 1 atm

이다.

실제 기체의 경우 분압을 퓨가시티로 대체하여 다음과 같이 나타낸다.

:

K_p =\prod \left[ \frac{f_i(x;T,p)}{p^\circ} \right]^{\nu_i}

3. 3. 산 해리 상수 (Ka)

산 해리 상수(영어: acid dissociation constant, 기호 ''K''_a)는 산의 이온화 평형을 나타내는 평형 상수이며, 산의 세기를 나타내는 척도로 사용된다. Ka^영어 값이 클수록 이온화 경향이 크다. 산 해리 상수는 온도에 의해서만 변한다.^[1] 산 이온화 상수라고도 한다.^[1]

Ka^영어 값만 비교하면 이온화가 잘 되는 순서, 즉 산의 세기가 강한 순서를 알 수 있다. 이온화가 여러 단계로 일어나는 경우에는 각 단계마다 산 해리 상수를 나타낼 수 있다. 예를 들어 아세트산이 물 속에서 이온화하면 각 성분의 농도가 일정하게 유지되는데, 이때 산 해리 상수는 평형 상수와 같이 온도에 의해서만 변한다.^[1]

산을 HA로 나타내고, 그 이온화 평형을 HA ↔ H⁺ + A^- 로 나타낼 때, 산 해리 상수 ''K''_a는 다음과 같이 나타낼 수 있다.^[1]

:

K_a=\frac{[H^+] [A^-]}{[HA]}

유기화학 및 생화학에서는 산 해리 평형에 대해 p''K''_a 값을 사용하는 것이 관례이다.^[2]

:

\mathrm{p}K_\mathrm{a}=-\log K_{\mathrm{diss}} = \log \left(\frac{1}{K_\mathrm{diss}}\right)\,

여기서 ''log''는 밑이 10인 로그 또는 상용로그를 나타내고, ''K''_diss는 단계적인 산 해리 상수이다. 염기의 경우 염기 결합 상수인 p''K''_b를 사용한다. 주어진 산이나 염기에 대해 p''K''_a + p''K''_b = p''K''_w의 관계가 있으므로, 계산에는 항상 p''K''_a를 사용할 수 있다.^[2]

pH는 수소 이온의 활동도로 정의된다.^[3]

:pH = −log₁₀ {H⁺}

이상적인 거동에 대한 근사치에서 활동도는 농도로 대체된다. pH는 유리 전극을 사용하여 측정되며, 브뢴스테드 상수라고도 알려진 혼합 평형 상수가 나타날 수 있다.^[3]

:HL L + H;

\mathrm{p}K =-\log \left(\frac{[\mathrm{L}]\{\mathrm{H}\}}{[\mathrm{HL}]} \right)

이는 전극이 알려진 활동도 또는 알려진 농도의 용액을 참조하여 교정되는지 여부에 따라 달라진다. 전극이 알려진 수소 이온 농도를 기준으로 교정되는 경우 pH가 아닌 p[H]를 쓰는 것이 더 좋지만, 이러한 제안은 일반적으로 채택되지 않는다.^[3]

3. 4. 염기 해리 상수 (Kb)

생화학에서는 완충 용액을 사용하여 pH를 고정한 상태에서 평형 상수를 측정하는 경우가 많다. 이때 측정되는 상수는 조건적 상수이며, 사용되는 완충 용액에 따라 다른 값을 가질 수 있다.^[8]

3. 5. 용해도곱 상수 (Ksp)

포화용액에서 염을 구성하는 양이온과 음이온의 농도를 곱한 값을 말한다. 보통 '''K_sp'''로 표시한다. 예를 들어 Ag^+(aq) + Cl^-(aq) -> AgCl(s) 반응에서 AgCl(s)은 대표적인 앙금이다. 이때, [Ag⁺] = 1.33×10⁻⁵이다. 이로부터 용해도를 계산하면, 1.923g/물 100g (20°C)이다. 따라서 평형 상수 K = [Ag⁺][Cl^-] = 1.77×10^-10이므로,

K_{sp}

= 1.77×10^-10의 용해도곱 상수값을 가진다.

3. 6. 가수분해 상수 (Kh)

중화 반응으로 생긴 염이 다시 이온화하여 생기는 가수분해 반응의 평형 상수를 말한다.^[7] 약한 염기인 암모니아와 강한 산 염화 수소의 중화로 생기는 염화 암모늄(NH₄Cl)에서 NH₄⁺은 다음과 같이 가수분해된다.

: NH₄⁺ + H₂O ⇄ NH₃ + H₃O⁺

이때 가수분해 상수(K_h)는 다음과 같다.

: K_h = [NH₃][H₃O⁺] / [NH₄⁺]

한편, 수용액 속에서 암모니아의 이온화 상수(K_b)와 물의 이온곱(K_w)은 다음과 같다.

: K_b = [NH₄⁺][OH^-] / [NH₃]

: K_w = [H₃O⁺][OH^-]

따라서, K_h, K_b, K_w 사이에는 다음과 같은 관계가 성립한다.

: K_hK_b = K_w

즉, 가수분해 상수 K_h는 K_b가 작을수록 커진다. 이러한 관계는 약한 산과 강한 염기 사이의 중화 반응에서도 성립한다.

아세트산나트륨과 같이 약한 산과 강한 염기 사이에서 형성된 염을 물에 녹이면, 약한 산의 짝염기인 아세트산 이온(CH₃COO^-)은 어느 정도 강한 염기이므로 수용액 속에서 수산화 이온(OH^-)을 형성한다.

: CH₃COO^- + H₂O ⇄ CH₃COOH + OH^-

일반적으로 약한 산의 짝염기(A^-)의 가수분해 반응의 평형 상수(K)는 다음과 같이 나타낼 수 있다.

: A^- + H₂O ⇄ HA + OH^-

이때 평형 상수는 K_a가 작을수록 큰 값을 갖는다. 즉, 음이온은 그 짝산이 약한 산일수록 가수분해 반응을 잘하며, 염기성 용액을 만든다. 반대로 양이온은 그 짝염기가 약한 염기일수록 가수분해 반응을 잘하여 산성 용액을 만든다.

수용액에서 수산화물 이온의 농도는 수소 이온의 농도와 다음과 같은 관계를 갖는다.

: K|W^영어 = [H⁺][OH^-]

: [OH^-] = K|W^영어[H⁺]^-1

금속 이온 가수분해의 첫 번째 단계는 다음과 같이 두 가지 방법으로 표현할 수 있다.

: β|*^영어 = KK_W

가수분해 상수는 일반적으로 β|*^영어 형태로 보고되므로 값이 1보다 훨씬 작은 경우가 많다. 예를 들어 log K = 4이고 log K_W = -14이면, log β|*^영어 = 4 + (-14) = -10이므로 β|*^영어 = 10^-10이다. 일반적으로 가수분해 생성물에 n개의 수산화기가 포함되어 있으면 log β|*^영어 = log K + n log K_W이다.

3. 7. 기타 평형 상수

이온 교환 반응에서 이온 A''ⁿ''^＋, B''^m''^＋가 관여하는 경우, 다음과 같은 평형이 성립한다.

:mAR + nB^(m+) <-> nBR. + mA^(n+)

이에 대한 교환 평형 상수 ''K''는 질량 작용의 법칙에 따라 다음과 같이 정의된다.^[4]

:

K=\frac{a_(BR)^n\bullet a_A^m}{a_B^n\bullet a_(AR)^m}

여기서 ''a''_AR, ''a''_BR은 교환 흡착된 이온의 활동도이고, ''a''_A, ''a''_B는 용액 속 이온의 활동도이다. 이론적으로 ''K'' 값을 구할 수 있지만, 실제로는 수지상 내에 교환 흡착된 이온 외에 도난 흡착에 의해 침투된 이온이 존재하여 구별이 어렵고, 활동도 계수도 불명확하여 ''K'' 값을 구하기 어렵다. 따라서 이온 교환 평형은 교환 흡착된 이온과 도난 흡착된 이온을 구별하지 않는 막평형의 관점에서 해석된다.

해양학에서는 온도, 압력, 염분에 따라 달라지는 혼용된 평형 상수 ''K''’를 사용한다.^[2] 온도가 낮아지거나 압력이 커지면 ''K''’는 작아지고, 염분이 줄어들어도 ''K''’는 작아진다. 해양에서는 복잡한 배경 매질 때문에 인공 해수를 이용해 구한 ''K''’ 값이 많이 사용되지만, 앞으로는 천연 해수에 대한 값을 사용해야 한다. 실제 열역학에서는 활동도를 사용하지만, 해양학에서는 활동도와 농도를 혼용하는 경우가 많으며, 활동도는 주로 pH에만 국한되어 사용된다.^[2]

누적 상수 (''β'')는 시약으로부터 착물이 형성되는 반응에 대한 상수이다. 예를 들어 ML₂ 형성에 대한 누적 상수는 다음과 같다.

:M + 2 L ML₂; [ML₂] = ''β''₁₂[M][L]²

단계적 상수 ''K''는 ML과 L로부터 같은 착물이 형성되는 반응에 대한 상수이며, 다음과 같다.

:ML + L ML₂; [ML₂] = ''K''[ML][L] = ''Kβ''₁₁[M][L]²

따라서 ''β''₁₂ = ''Kβ''₁₁ 관계가 성립한다. 누적 상수는 항상 단계적 상수의 곱으로 표현할 수 있다.

비대칭 분자에서 두 개 이상의 부위가 평형 반응에 관여하는 경우, 여러 개의 미시 상수(micro-constant)가 존재할 수 있다. 예를 들어, L-DOPA (LH₂)는 두 개의 비등가 하이드록실기를 가지므로, 다음과 같이 여러 종이 생성될 수 있다.

LH 종의 농도는 두 미시종 L¹H와 L²H 농도의 합과 같다. 상수 ''K''₂는 두 미시종을 생성물로 하는 반응에 대한 것이므로, [LH] = [L¹H] + [L²H]가 분자에 나타나고, 거시 상수(macro-constant) ''K''₂는 두 미시 상수 ''k''₂₁와 ''k''₂₂의 합과 같다.

:''K''₂ = ''k''₂₁ + ''k''₂₂

반면, 상수 ''K''₁은 두 미시종을 반응물로 하는 반응에 대한 것이므로, [LH] = [L¹H] + [L²H]는 분모에 나타난다.^[4]

:1/''K''₁ = 1/''k''₁₁ + 1/''k''₁₂

따라서 ''K''₁ = ''k''₁₁ ''k''₁₂ / (''k''₁₁ + ''k''₁₂).

이 예에서 네 개의 미시상수가 존재하며, 두 가지 제약 조건이 있다. 실험 데이터로부터는 K₁과 K₂에 대한 두 개의 거시상수 값만 얻을 수 있다. 미시상수 값은 적외선 분광법 등으로 결정할 수 있지만, 화학적 또는 수학적 방법을 통해 추정하기도 한다.^[5]^[6] L-DOPA의 경우, 이성질체화 상수가 0.9로 추정되어, 미시종 L¹H와 L²H는 모든 pH 값에서 거의 동일한 농도를 갖는다.

pH는 수소 이온 활동도의 로그값으로 정의된다.

:pH = −log₁₀ {H⁺}

이상적인 경우 활동도는 농도로 대체된다. pH는 유리 전극으로 측정되며, 혼합 평형 상수가 나타날 수 있다.

:HL L + H;

\mathrm{p}K =-\log \left(\frac{[\mathrm{L}]\{\mathrm{H}\}}{[\mathrm{HL}]} \right)

전극 교정에 따라 평형 상수는 농도 비율이 될 수 있다.

4. 평형 상수의 성질

평형 상수는 온도에 의존하며, 압력이나 농도에는 영향을 받지 않는다. 정반응과 역반응의 평형 상수는 서로 역수 관계이다. 즉, 정반응의 평형 상수가 K_c이면, 역반응의 평형 상수는 1/K_c이다. K_c 값이 크면 정반응이 많이 진행된다는 의미이고, K_c의 역수는 작은 값을 가지므로 역반응은 거의 진행되지 않는다.^[1]

전체 반응이 여러 단계로 이루어져 있을 때, 전체 반응의 평형 상수는 각 단계 반응의 평형 상수의 곱과 같다. 예를 들어, 전체 반응이 n개의 단계로 이루어져 있다면, 전체 평형 상수 K_전체는 다음과 같이 표현된다.

:K_전체=K₁×K₂×K₃×∙∙∙ ×K_n

화학 반응식의 계수가 변하면 평형 상수 값도 변한다. 일반적으로 균형 반응식의 모든 계수에 n을 곱하면, 평형 상수는 K' = Kⁿ과 같이 지수로 나타난다.^[1]

4. 1. 반응 지수 (Q)

화학 반응이 아직 평형에 도달하지 않은 상태일 때, 처음 농도를 평형 상수 수식에 넣어 얻어진 양을 '''반응 지수'''(reaction quotient|리액션 쿼션트^영어)라고 한다. 반응 지수와 평형 상수 값을 비교하여 알짜 반응이 평형에 이르기까지 진행할 방향을 예측할 수 있다.^[1]

< : 반응물에 대한 생성물의 초기 농도의 비가 너무 작다. 평형에 이르기 위해서는 반응물이 생성물로 전환되어야 한다. 계는 평형에 이르도록 왼쪽에서 오른쪽으로(반응물을 소모하여 생성물을 생성하면서) 진행한다.
= : 초기 농도가 평형 농도이다. 계는 평형 상태에 있다.
> : 반응물에 대한 생성물의 초기 농도의 비가 너무 크다. 평형에 이르기 위해서는 생성물이 반응물로 전환되어야 한다. 계는 평형에 이르도록 오른쪽에서 왼쪽(생성물을 소모하여 반응물을 생성하면서) 진행한다.

4. 2. 불균일 평형

불균일 평형(heterogeneous equilibrium)은 서로 다른 상에 있는 반응물과 생성물이 관련된 가역 반응이다. 예를 들어, 탄산 칼슘을 밀폐 용기에서 가열하면 다음과 같은 평형을 이룬다.

:CaCO3(s) <-> CaO(s) + CO2(g)

두 개의 고체와 하나의 기체가 세 개의 분리된 상을 이루고 있다. 이때 평형 상수는 다음과 같이 나타낼 수 있다.

:

K_c = \frac{[CaO][CO_2]}{[CaCO_3]}

그러나 밀도와 마찬가지로 고체의 "농도"는 세기 성질이므로 물질의 양에 좌우되지 않는다. 따라서

[CaO]

와

[CaCO_3]

항은 상수이므로, 평형 상수 식을

K_c = [CO_2]

와 같이 간단하게 표기할 수 있다.

활동도로 바꾸면 더 단순해진다. 열역학에서 순수한 고체의 활동도는 1이다. 마찬가지로 순수한 액체의 활동도도 1이다. 따라서 반응물이나 생성물이 고체 또는 액체라면 평형 상수 식에서 생략할 수 있다.^[1]

4. 3. 아레니우스 식

평형 상수는 아레니우스 식을 통해 온도에 따른 변화를 예측할 수 있다. 아레니우스 식은 다음과 같다.

:

k=Ae^{-E_a/RT}

A: 빈도 인자 (유효 충돌 빈도)
E_a: 활성화 에너지
R: 기체 상수 (8.3145J/K∙mol)
T: 절대 온도

특정 온도 T₁에서의 평형 상수 값 K₁을 이용하여 다른 온도 T₂에서의 평형 상수 K₂를 구하는 식은 다음과 같다.

:

ln K_2 - lnK_1 = -\frac{\bigtriangleup_r H^\circ }{R}(\frac{1}{T_2}-\frac{1}{T_1})

여기서 ∆_r H°는 표준 반응 엔탈피 변화를 나타내며, 온도에 따라 크게 변하지 않는다고 가정한다. 이 식은 반트호프 방정식을 적분하여 얻을 수 있다.^[13]

르샤틀리에 원리에 따르면, 발열 반응 (ΔH < 0)의 경우 온도가 증가하면 K는 감소하고, 온도가 감소하면 K는 증가한다. 흡열 반응의 경우에는 반대로 작용한다.

5. 평형 상수의 활용

평형 상수를 통해 평형 상태에서의 반응 혼합물의 조성을 예측할 수 있다. 평형 상수는 헤모글로빈에 의한 산소 운반, 인체의 산-염기 항상성과 같은 생화학적 과정뿐만 아니라, 화학 공정에서 최적의 반응 조건을 설정하고 수율을 예측하는 등 다양한 분야에서 활용된다.^[1]

5. 1. 생화학적 과정

생화학에서 평형 상수는 혈액 속 헤모글로빈에 의한 산소 운반, 인체의 산-염기 항상성 등 여러 생화학적 과정을 이해하는 데 필수적이다.^[1]

5. 2. 산업적 응용

화학 공정에서 최적의 반응 조건을 설정하고 수율을 예측하는 데 평형 상수가 활용된다. 표준 평형 상수는 다음과 같이 정의된다.^[1]

:

K^\circ =\exp\left[ -\frac{\Delta_\text{r}G^\circ}{RT} \right]

기체의 화학 반응이 평형 상태에 있을 때

K^\circ =K_p

가 성립한다.^[1] 또한, 용액의 화학 반응이 평형 상태에 있을 때

K^\circ =K_c

가 성립한다.^[1]

6. 평형 상수의 측정 및 계산

화학 평형 상태에서 정반응과 역반응의 속도는 같고, 반응 혼합물의 조성은 시간에 따라 변하지 않는다. 이때 반응에 대한 깁스 자유 에너지 변화( $\Delta G$ )는 0이다. 평형 상수는 평형 상태의 혼합물 조성과 관련이 있으며, 다음과 같이 나타낼 수 있다.^[1]^[2]

: $K^\ominus = \frac^\rho \mathrm{\{S\}}^\sigma...}}^\alpha \mathrm{\{B\}}^\beta...}} = \frac^\rho ^\sigma ... } ^\alpha ^\beta ...} \times \Gamma,$

: $\Gamma= \frac{\gamma_R^\rho \gamma_S^\sigma...}{\gamma_A^\alpha \gamma_B^\beta...},$

여기서 {X}는 시약 X의 열역학 활동도, [X]는 농도의 수치 값^[3], γ는 활동도 계수를 나타낸다. 기체의 경우 [X] 대신 부분압( $P_X$ )의 수치 값을 사용한다.^[3]

평형 상수( $K^\ominus$ )는 표준 깁스 자유 에너지 반응 변화( $\Delta G^\ominus$ )와 다음과 같은 관계를 갖는다.

: $\Delta G^\ominus = -RT \ln K^\ominus,$

여기서 ''R''은 기체 상수, ''T''는 절대 온도(단위: 켈빈)이다.

평형 상수는 반응의 정반응 및 역반응 속도 상수(''k''_f 및 ''k''_r)와 다음과 같이 관련된다.

: $K^\ominus = \frac{k_\text{f}}{k_\text{r}}.$

활동도 계수를 실험적으로 알 수 없는 경우, 다음과 같은 방법으로 평형 상수를 근사할 수 있다.^[10]^[11]

계산된 활동도 계수와 반응물의 농도를 함께 사용한다.
모든 활동도 계수가 1이라고 가정한다. (모든 농도가 매우 낮을 때)
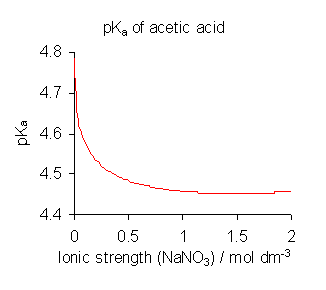
높은 이온 세기의 매질을 사용하여 활동도 계수의 영향을 최소화한다.

표준 반응 깁스 에너지를 이용하면 표준 평형 상수는 다음과 같다.

:

K^\circ =\exp\left[ -\frac{\Delta_\text{r}G^\circ}{RT} \right]

기체의 화학 반응이 평형 상태에 있을 때

K^\circ =K_p

가 성립한다. 또한, 용액의 화학 반응이 평형 상태에 있을 때

K^\circ =K_c

가 성립한다.

6. 1. 온도 의존성

반응물과 생성물의 표준 몰 깁스 자유 에너지 차이를 표준 반응 깁스 에너지라고 하며, 평형 상태에서 이 값은 0이다. 평형 상태에서 부분 압력의 비는 K로 나타낸다.^[9]

어느 한 온도 T₁에서의 평형 상수 값 K₁을 이용하여 다른 온도 T₂에서의 평형 상수 K₂를 구하기 위해 다음 식을 사용한다.

:

ln K_2 - lnK_1 = -\frac{1}{R}\int_{1/T_1}^{1/T_2} \bigtriangleup_r H^\circ d(1/T)

∆_r H° (표준 반응 엔탈피 변화)가 온도에 거의 의존하지 않는다면, 위 식은 다음과 같이 간단하게 표현된다.^[13]

:

ln K_2 - lnK_1 = -\frac{\bigtriangleup_r H^\circ }{R}(\frac{1}{T_2}-\frac{1}{T_1})

이 식은 반트 호프 식이라고 불리며, 특정 온도에서의 평형 상수 값을 통해 다른 온도에서의 평형 상수 값을 계산할 수 있게 해준다.

반트 호프 식에 따르면, 발열 반응 (ΔH < 0)에서는 온도가 증가하면 K 값이 감소하고, 온도가 감소하면 K 값이 증가한다. 이는 르 샤틀리에 원리와 일치한다. 흡열 반응의 경우에는 반대로 온도가 증가하면 K 값이 증가하고, 온도가 감소하면 K 값이 감소한다.

표준 열역학적 논의에 따르면 엔탈피는 온도에 따라 변한다.^[14]

:

\left(\frac{\partial H}{\partial T}\right)_p = C_p

여기서 C_p는 일정 압력에서의 열용량이다.

표준 열역학적 성질을 알고 있다면, 특정 온도에서의 ''K'' 값을 다른 주어진 온도에서의 ''K'' 값으로부터 계산할 수 있다. 평형 상수에 대한 온도의 영향은 깁스 에너지에 대한 온도의 영향과 같다.

:

\ln K =

여기서 Δ_r''G''^o는 반응 표준 깁스 에너지이며, 반응 생성물의 표준 깁스 에너지 합에서 반응물의 표준 깁스 에너지 합을 뺀 값이다.

표준 깁스 에너지는 다음과 같이 나타낼 수 있다.^[15]

:

G_{T_2}^\ominus = G_{T_1}^\ominus-S_{T_1}^\ominus(T_2-T_1)-T_2 \int^{T_2}_{T_1} \,dT + \int^{T_2}_{T_1} C_p^\ominus\,dT

깁스 에너지에 대한 온도의 영향은 전적으로 열용량에 기인한다. 열용량의 온도 의존성을 알면 위 식의 적분을 계산할 수 있다.

표준 몰 열용량 ''C''를 온도의 해석 함수(예: 쇼메이트 방정식)로 근사하면, 적분을 풀어 다른 매개변수를 계산하는 해석적 표현을 얻을 수 있다.^[16]

6. 2. 동위원소 치환 효과

동위원소 치환, 특히 수소가 중수소(또는 삼중수소)로 치환될 경우 평형 상수 값의 변화가 나타날 수 있다.^[19] 이러한 ''평형 동위원소 효과''는 주로 동위원소 치환에 따른 질량 변화로 인해 H–X 결합의 영점 진동 에너지가 변화하기 때문에 발생한다.^[19] 영점 에너지는 진동하는 수소 원자 질량의 제곱근에 반비례하므로, D–X 결합의 영점 에너지가 H–X 결합보다 더 작다.

예를 들어 R' + H–R R'–H + R과 같은 수소 원자 추출 반응과 평형 상수 K_H를 생각해 보자. 여기서 R'과 R은 유기 라디칼이며, R'이 R보다 수소와 더 강한 결합을 형성한다. 중수소 치환으로 인한 영점 에너지 감소는 R'–H에서 R–H보다 더 중요하며, R'–D가 R–D보다 더 안정화되므로 R' + D–R R'–D + R의 평형 상수 K_D는 K_H보다 크다. 이는 ''더 무거운 원자가 더 강한 결합을 선호한다''는 규칙으로 요약할 수 있다.^[19]

용액에서도 비슷한 효과가 나타나는데, 이는 약한 수용액 산에서 용매 분자로 H⁺ 또는 D⁺의 이동을 설명하는 산 해리 상수(K_a)에 해당한다. HA + H₂O H₃O⁺ + A⁻ 또는 DA + D₂O D₃O⁺ + A⁻ 반응에서, 중수소화된 산은 중수에서 연구된다. 그 이유는 일반적인 물에 용해될 경우 중수소가 용매 속 수소와 빠르게 교환되기 때문이다.^[19]

생성물 종 H₃O⁺(또는 D₃O⁺)는 용질 산보다 더 강한 산이므로 더 쉽게 해리되며, 그 H–O(또는 D–O) 결합은 용질 산의 H–A(또는 D–A) 결합보다 약하다. 따라서 동위원소 치환으로 인한 영점 에너지 감소는 D₃O⁺보다 DA에서 덜 중요하므로 K_D < K_H가 되며, D₂O 속 중수소화된 산은 H₂O 속 비중수소화된 산보다 약하다. 많은 경우 로그 상수의 차이 pK_D – pK_H는 약 0.6이며,^[19] 중수소화된 산의 50% 해리에 해당하는 pD는 비중수소화된 산의 50% 해리에 대한 pH보다 약 0.6 단위 더 높다.

비슷한 이유로 중수의 자동 이온화는 동일한 온도에서 일반적인 물보다 작다.

7. 추가 개념

안정도 상수, 형성 상수, 결합 상수, 해리(이온화) 상수는 모두 평형 상수의 일종이다.^[1] 이온화 상수는 이온화 반응의 평형 상수를 나타내며, 기호로는 K_d로 표시한다.^[2]

전해질이 수용액 속에서 이온화되는 정도를 나타내는 수치로, 이 값이 작을수록 이온화가 잘 일어나지 않는 약전해질임을 의미한다. 예를 들어 전해질 AB가 수용액에서 이온화될 때 (AB ↔ A⁺ + B^-), 각 농도를 [AB], [A⁺], [B^-]라고 하면, 이온화 상수는 다음과 같다.

:K = [A⁺] [B^-]/[AB]

일반적으로 너무 작은 수이므로 역로그 값을 취해 pK_d로 표시한다.

:pK_a=-logK_a

유기화학 및 생화학에서는 산 해리 평형에 대해 p''K''_a 값을 사용하는 것이 일반적이다.

: $\mathrm{p}K_\mathrm{a}=-\log K_{\mathrm{diss}} = \log \left(\frac{1}{K_\mathrm{diss}}\right)\,$

여기서 ''log''는 상용로그를 나타내고, ''K''_diss는 단계적인 산 해리 상수이다. 염기의 경우 염기 결합 상수인 p''K''_b를 사용한다. 주어진 산이나 염기에 대해 p''K''_a + p''K''_b = p''K''_w 관계가 있으므로, 계산에는 항상 p''K''_a를 사용할 수 있다.

반면, 금속 착물의 안정도 상수와 포접 착물의 결합 상수는 일반적으로 결합 상수로 표현된다.

참조

_[1] 웹사이트 IUPAC Gold Book https://goldbook.iup[...]
_[2] 서적 The Determination of Stability Constants McGraw-Hill 1961
_[3] 서적 Chemical Principles Freeman 2016
_[4] 논문 The spectrum of a dissociation intermediate of cysteine: a biophysical chemistry experiment 1988-02-01
_[5] 논문 Protonation sequence of linear aliphatic polyamines by 13C NMR spectroscopy 1994
_[6] 논문 A Cluster Expansion Method for the Complete Resolution of Microscopic Ionization Equilibria from NMR Titrations 2000
_[7] 서적 The Hydrolysis of Cations Wiley 1976
_[8] 서적 Complexometric titrations Methuen 1969
_[9] 서적 The principles of chemical equilibrium Cambridge University Press 1981
_[10] 서적 Ionic Equilibrium John Wiley and Sons 1998
_[11] 웹사이트 Project: Ionic Strength Corrections for Stability Constants https://web.archive.[...] International Union of Pure and Applied Chemistry 2008-11-23
_[12] 간행물 Green Book (IUPAC), Quantities, Units and Symbols in Physical Chemistry https://iupac.org/wp[...] 2007
_[13] 서적 Physical Chemistry https://archive.org/[...] Oxford 2006
_[14] 논문 Ligands containing elements of group VIB. Part V. Thermodynamics of silver complex formation of some saturated and unsaturated (alkyl-thio)acetic and (alkylseleno)acetic acids 1971
_[15] 서적 Aqueous Systems at Elevated Temperatures and Pressures: Physical Chemistry of Water, Steam and Hydrothermal Solutions Elsevier 2004
_[16] 서적 Handbook of Corrosion Engineering McGraw-Hill 2011-11
_[17] 서적 Physical Chemistry Oxford University Press 1978
_[18] 논문 Activation and reaction volumes in solution. 2 1989
_[19] 서적 Chemical Kinetics Harper & Row 1987
_[20] 문서 『学術用語集物理学編』
_[21] 문서 IUPAC ''Goldbook''
_[22] 웹사이트 平衡定数・会合定数・解離定数・結合定数について分かりやすく解説 http://chemblogno1.b[...] 2019-10-04
_[23] 서적 The Determination of Stability Constants McGraw-Hill 1961

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com